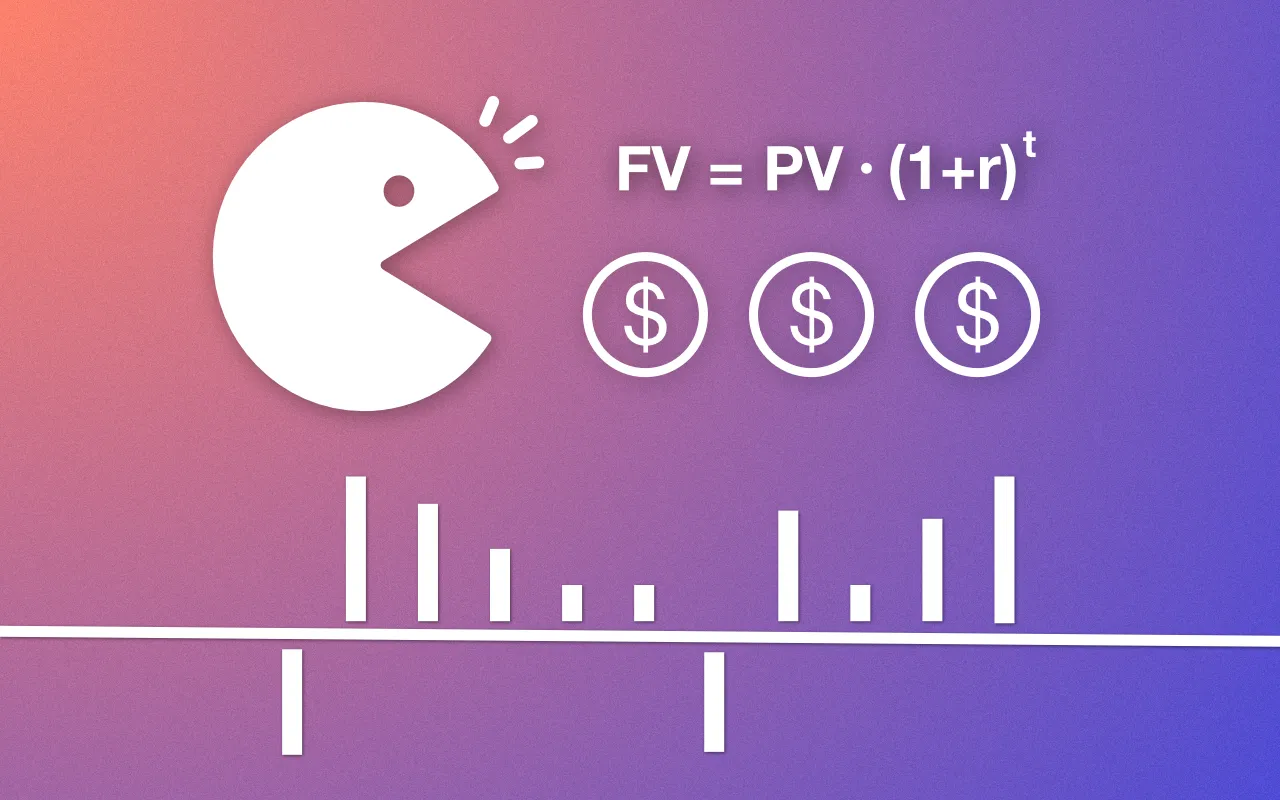
Time Value of Money and how inflation, interest and uncertainty devaluate our future income

Time value of money is a fundamental concept in finance stating that money on hand today is more valuable than the same money in the future. It sits at the heart of financial decisions made by individuals, organizations, and governments.

In this article, we dive into the three main drivers of the time value of money

1. Inflation
2. Interest
3. Uncertainly

and walkthrough hands-on examples from our day-to-day lives to illustrate how these three factors shape financial decisions.

Inflation

Normally, the economy is in a state of inflation which means that prices for goods and services increase as time passes. In other words, our money has less purchasing power in the future than it does today. For example, suppose a slice of pizza 🍕 costs $\$10$ today and that the inflation rate is $2\%$ (which is the target inflation set by central banks in many countries, such as FED in the USA and Riksbanken in Sweden). Next year, the same slice of pizza will cost

$$\$10\cdot(1+0.02)=\$10.2.$$

Conversely, if we look at purchasing power, we see that $\$10.2$ in our bank account today is worth

$$\frac{\$10.2}{1+0.02}= \$10$$

in a year from now. So much for that pizza 🫠

What about deflation? When the economy is in a state of deflation, prices decrease over time. If we assume a deflation rate of $2\%$, all the inflation example above are reversed. The slice of pizza 🍕 will cost $\frac{\$10}{1+0.02}\approx \$9.8$ and if you hold on to your $\$10$ the future purchasing power of your money will be the same as $\$10\cdot (1+0.02)=\$10.2$ today. However, deflation is quite uncommon, and when it does occur, it is desirable to find a way out of it in order to avoid dangerous deflationary spirals that can lead countries into deep recessions.

You can imagine how unnatural deflation feels when you think of it as a state where everyone is saying, “I won’t buy anything today because prices will drop tomorrow. I also won’t buy anything the day after tomorrow because prices will drop even more.”

On the other hand, when prices stay the same or increase, it feels more in line with our everyday experience of the economy. Therefore, inflation is one of the core drivers of the time value of money.

Interest

Money on hand today can be placed in accounts that yield interest. For example, we could deposit our money in a 3-month fixed-rate savings account. During the following three months, our money is locked away, and in return, the bank pays out interest at the end of the term (aka. at maturity). Let’s say we have $\$1000$ to deposit and the the bank offers a fixed rate of $3\%$. Usually, rates refer to annual rates. In order to get the monthly interest we must divide by $12$, which gives as a monthly rate rate of $\frac{3\%}{12}=0.25\%$ a and the quarterly interest rate is $0.25\%\cdot 3=0.75\%$. At the end of the term (three months later) we get back our initial deposit, $\$1000$, plus the earned interest

$$\$1000 \cdot 0.0075=\$7.5.$$

It might not seem like much, however, if the bank keeps offering the annual rate $2.5\%$ each term and we repeat this process every quarter (three months), the interest compounding effect kicks in. Our initial $\$1000$ becomes $\$1007.5$ after the first term. Next period we deposit $\$1007.5$ and earn

$$\$1007.5 \cdot 0.0075 \approx \$7.6$$

in interest. Six months later, we have $\$1015.1$. This can be repeated two more times in a year for a total of four terms per year.

Suppose we do this over 20 years. How much would our initial deposit grow? Well, each year we can four terms. 20 years later this amounts to $20\cdot 4=80$ terms and our initial $\$1000$ becomes

$$\$1000 \cdot (1+0.0075)^{80} \approx \$1818.$$

A growth by almost $82\%$ which illustrates another reason for the time value of money. Keep in mind that this is a simplified illustration, we have assumed that the bank offers the same fixed-rate every period which isn’t true in general. The fixed-rate can increase and decrease significantly depending on the economic situation. It is also true that you can invest your money in assets that can provide a significantly larger growth, for instance, the stock market. On the other hand, the fixed-rate saving accounts risk-free meaning that as long as the bank is solvent, you are guaranteed to get back at least your inital deposit (if the fixed-rate is $0\%$), whereas in the stock market your initial $\$1000$ can both increase and decrease in value depending on the market condition.

Uncertainty

The value of money today is often influenced by how unpredictable the future seems, with risk playing a central role in financial decisions. When we’re unsure about future conditions, whether it’s inflation, interest rates, or economic stability, we tend to place more value on money today.

Let’s look at a simplified example to illustrate the point. Suppose we lend money to a friend who promises to repay us at some point in the future. If this friend is known for being unreliable, the future value of that promise begins to shrink. The more unpredictable their actions, the less we trust that future payment. As uncertainty grows, the value of that money decreases over time.

A similar dynamic occurs in economies experiencing high inflation or instability, where the future purchasing power of money becomes less certain. In such a scenarios, central banks often lower interest rates to stimulate the economy, which, as we discussed in the previous section, causes the time value of money to decrease due to lower investment potential. This is also true in an unpredictable global landscape, where geopolitical events or shifts in global markets can add further uncertainty, diminishing the future value of money.

Share article