Why a dollar today beats a dollar tomorrow: Inflation, interest, and uncertainty explained

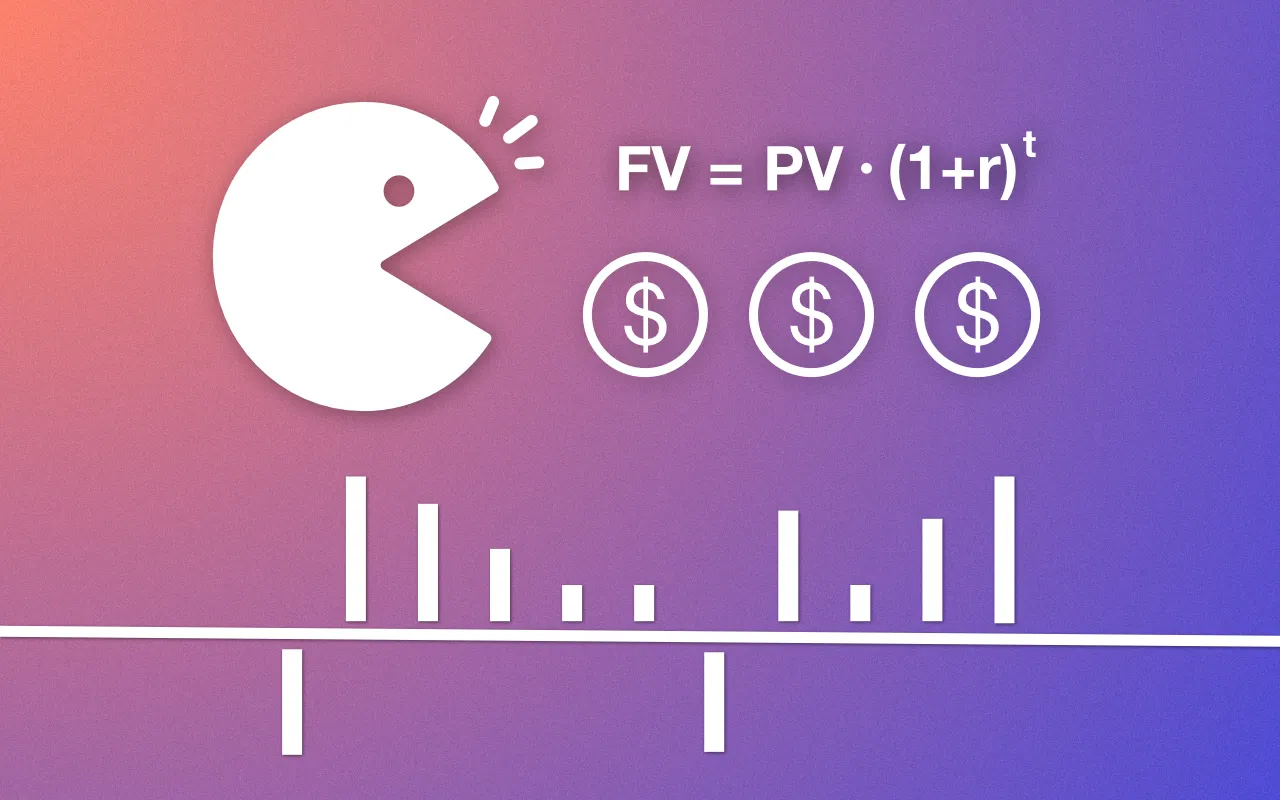
The time value of money is a fundamental financial principle stating that a dollar today is worth more than the same dollar in the future. This idea underpins many financial decisions made by individuals, organizations, and governments.

In this article, we break down the three core drivers of the time value of money:

1. Inflation - the gradual loss of purchasing power
2. Interest - the opportunity to grow money over time
3. Uncertainly - the risk that the future may not unfold as expected

By understanding how these forces interact, we’ll gain a clearer framework for evaluating financial decisions today versus tomorrow.

Inflation: Why money buys less over time

Inflation quietly erodes purchasing power, making it one of the most intuitive drivers of the time value of money. Normally, the economy is in a state of inflation which means that prices for goods and services increase as time passes. In other words, our money has less purchasing power in the future than it does today. For example, suppose a slice of pizza 🍕 costs $\textcolor{dodgerblue}{\$10}$ today and that the inflation rate is $\textcolor{crimson}{2\%}$ (which is the target inflation set by central banks in many countries, such as FED in the USA and Riksbanken in Sweden). Next year, the same slice of pizza will cost

$$\textcolor{dodgerblue}{\$10}\cdot(1+\textcolor{crimson}{0.02})=\$10.2.$$

This is known as the future value of the pizza slice.

Conversely, if we look at purchasing power, we see that $\textcolor{mediumpurple}{\$10}$ in our bank account a year from now, will today be worth

$$\frac{\textcolor{mediumpurple}{\$10}}{1+\textcolor{crimson}{0.02}}\approx \$9.8.$$

This is known as the present value of holding $\$10$ a year from now.

In other words, $\$10$ today can get us a slice of pizza. However, that same $\$10$ a year from now will leave us $\$.20$ short due to inflation. So much for that pizza 🫠 That is why inflation is one of the drivers of the time value of money.

The above calculations can be summarized in the following general equations

$$\text{FV} = \text{PV} \cdot \bigg(1+\frac{r}{n}\bigg)^{t\cdot n}$$

where

• FV - stands for Future Value
• PV - stands for Present Value
• r - is the annual rate
• t - is the time in years
• n - number of compounding periods per year

For example, the pizza slice worth $\text{PV}_{🍕}=\textcolor{dodgerblue}{\$10}$ today with an inflation rate of $\textcolor{crimson}{2\%}$, will cost

$$\text{FV}_{🍕} = \textcolor{dodgerblue}{\$10} \cdot (1+\textcolor{crimson}{0.02})^{\textcolor{seagreen}{10}} \approx \$12.2$$

ten years ($\textcolor{seagreen}{t=10}$) from now. Since inflation is compounded annually, we used $n=1$ to compute the future value of the pizza slice. In the next section we see an example with quarterly compounding.

Interest: How money can grow over time

Interest drives the time value of money as an investment option. Money on hand today can be placed in accounts that yield interest payouts. For example, we could deposit our money in a 3-month fixed-rate savings account. During the following three months, our money is locked away, and in return, the bank pays out interest at the end of the term. While our money was locked away it lost value due to inflation. However, if the interest payouts are large enough they can both counteract the effects of inflation while providing financial growth.

Let’s say we have $\textcolor{dodgerblue}{\$1000}$ to deposit and the the bank offers a fixed rate of $3\%$. Usually, rates refer to annual rates. In order to get the monthly interest we must divide by $12$, which gives us a monthly rate of $3\%/12=0.25\%$ and the quarterly interest rate is $0.25\%\cdot 3=\textcolor{crimson}{0.75\%}$. At the end of the term (three months later) we get back our initial deposit, $\textcolor{dodgerblue}{\$1000}$, plus the earned interest

$$\textcolor{dodgerblue}{\$1000} \cdot \textcolor{crimson}{0.75\%}=\$7.5.$$

It might not seem like much, however, if the bank keeps offering the annual rate $2.5\%$ each term and we repeat this process every quarter (three months), the interest compounding effect kicks in. Our initial $\textcolor{dodgerblue}{\$1000}$ becomes $\textcolor{mediumpurple}{\$1007.5}$ after the first term. Next period we deposit $\$1007.5$ and earn

$$\textcolor{mediumpurple}{\$1007.5} \cdot \textcolor{crimson}{0.0075} \approx \$7.6$$

in interest. Six months later, we have $\$1015.1.$ This can be repeated two more times in a year for a total of four terms per year.

Suppose we do this over 20 years. How much would our initial deposit grow? Well, each year offers four terms and 20 years later this amounts to $20\cdot 4=\textcolor{seagreen}{80}$ terms and our initial $\textcolor{dodgerblue}{\$1000}$ becomes

$$\textcolor{dodgerblue}{\$1000} \cdot (1+\textcolor{crimson}{0.0075})^{\textcolor{seagreen}{80}} \approx \$1818.$$

A growth by almost $82\%$ which illustrates another reason for the time value of money.

Keep in mind that this is a simplified illustration, we have assumed that the bank offers the same fixed-rate every period which isn’t true in general. The fixed-rate can increase and decrease significantly depending on the economic situation. It is also true that you can invest your money in assets that can provide a significantly larger growth, for instance, the stock market. On the other hand, a fixed-rate savings account is low-risk meaning that as long as the bank is solvent, you are guaranteed to get back at least your initial deposit (if the fixed-rate is $0\%$), whereas in the stock market your initial $\textcolor{dodgerblue}{\$1000}$ can both increase and decrease in value depending on the market conditions.

In the previous example, we performed multiple calculations to arrive to the final future value of our initial deposit. We can achieve the same result in one step by utilizing the future value equation from the previous section with the following parameters

• Present value: $\text{PV}=\$1000$
• Annual interest: $r=3\%$
• Compounding time: $t=20$ years
• Compounding period: $n=4$ (quarterly)

$$\begin{align*} \text{FV} &= \textcolor{dodgerblue}{\$1000} \cdot\bigg(1+\frac{0.03}{4}\bigg)^{4\cdot 20} \\ &= \textcolor{dodgerblue}{\$1000} \cdot(1+\textcolor{crimson}{0.0075})^{\textcolor{seagreen}{80}} \\ &\approx \$1818. \end{align*}$$

Uncertainty: Why the future is always discounted

The value of money today is often influenced by how unpredictable the future seems, with risk playing a central role in financial decisions. When we’re unsure about future conditions, whether it’s inflation, interest rates, or economic stability, we tend to place more value on money today.

Let’s look at a simplified example to illustrate the point. Suppose we lend money to a friend who promises to repay us at some point in the future. If this friend is known for being unreliable, the future value of that promise begins to shrink. The more unpredictable their actions, the less we trust that future payment. As uncertainty grows, we place a lower present value on that future payment the further into the future it is.

A similar dynamic occurs in economies experiencing high inflation or instability, where the future purchasing power of money becomes less certain. In cases, central banks often lower interest rates to stimulate the economy , which, as we discussed in the previous section, causes the time value of money to decrease due to lower investment potential. This is also true in an unpredictable global landscape, where geopolitical events or shifts in global markets can add further uncertainty, diminishing the present value of future investment payouts.

Summary

The time value of money rests on three fundamental forces:

• Inflation steadily causes prices of goods and services to increase and the money we hold today has more purchasing power now than it ever will.
• Interest places an opportunity cost on spending today versus investing our money to earn returns later, hence, counter-balance the effects of inflation.
• Uncertainty reflects the reality that the future is never guaranteed, increasing the value we place on certainty today.

Balancing these forces is at the core of financial decision-making. Whether evaluating savings accounts, investments, loans, or long-term projects, understanding how inflation, interest, and uncertainty interact allows us to compare values across time in a meaningful way.

In future articles, we’ll explore the tools, formulas, and financial instruments used in practice to measure and manage the time value of money from discounting cash flows to valuing real-world investments.

Share article